Ознаки подібності трикутників

Перша ознака. Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого трикутника, то трикутники подібні.

Друга ознака. Якщо дві сторони одного трикутника відповідно пропорційні двом сторонам іншого трикутника, а кути між цими сторонами рівні, то трикутники подібні.

Третя ознака. Якщо три сторони одного трикутника відповідно пропорційні трьом сторонам іншого трикутника, то трикутники подібні.

Чотирикутник називається опуклим, якщо він міститься в одній півплощині відносно кожної прямої, якій належить його сторона.

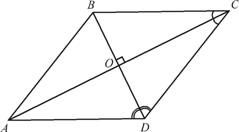
Ромбом називається паралелограм, усі сторони якого рівні між собою.

Крім властивостей паралелограма ромб (див. рисунок) має свої окремі властивості:

а) кожна діагональ ромба є бісектрисою його кутів;

б) діагоналі ромба взаємно перпендикулярні.

Прямокутником називається паралелограм, усі кути якого прямі.

Окрема властивість прямокутника: діагоналі прямокутника рівні між собою.

Звідси випливає важлива властивість прямокутного трикутника:

Медіана прямокутного трикутника, проведена з вершини прямого кута, дорівнює половині гіпотенузи.

Квадратом називається ромб, усі кути якого прямі.

Коло і круг. Число π

Колом називають множину точок площини, рівновіддалених від однієї точки, яку називають центром кола.

Кругом називають множину точок площини, відстань яких від однієї точки — центра кола — не перевищує сталої величини, яку називають радіусом кола.

Дотичною називають пряму, що має з колом одну спільну точку (рис. 1). Січною називають пряму, що має дві спільні точки з колом.

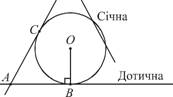
Рис. 1

Хордою називають відрізок, що сполучає дві точки кола.

Діаметром називають хорду, що проходить через центр кола.

Теорема 1. Дотична перпендикулярна до радіуса, проведеного в точку дотику.

Обернена теорема: якщо пряма перпендикулярна до радіуса в його кінці, що лежить на колі, то вона є дотичною (див. рис. 1).

Теорема 2. Відрізки дотичних, проведених до кола з однієї точки, що лежить поза колом, рівні між собою (на рис. 1 АВ = АС).

Теорема 3. Діаметр кола, перпендикулярний до хорди, проходить через її середину.

Довжина кола С = 2πR, а площа круга S = πR², де R — радіус кола, π = 3,14159... .

Теорема Піфагора. Якщо трикутник прямокутний, то сума квадратів катетів дорівнює квадрату гіпотенузи:

а² + b² = c²,

де а = ВC, b = AC, c = АВ (рис. 1).

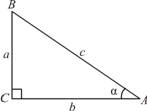
Рис. 1

Обернена теорема: Якщо сума квадратів двох сторін трикутника дорівнює квадрату третьої сторони, те цей трикутник прямокутний.

За допомогою теореми Піфагора доводяться наведені далі твердження.

1. У рівнобедреному прямокутному трикутнику гострі кути дорівнюють по 45°, а відношення гіпотенузи до катета дорівнює

2. Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи.

Теорема косинусів. Квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін мінус подвоєний добуток цих сторін на косинус кута між ними (рис. 2):

с² = а² + b² – 2abcos γ.

Теорема синусів. Відношення сторони трикутника до синуса протилежного кута є величина стала для даного трикутника, що дорівнює двом радіусам описаного кола (рис. 2):

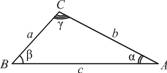
Рис. 2

Формули для обчислення площі трикутника (рис. 2)

(1)

(2)

(3)

(4)

(5)

де h_a — висота, опущена на сторону a; r — радіус уписаного кола; R — радіус описаного кола; р — напівпериметр. Формула (5) називається формулою Герона.

Площа чотирикутника

де d₁ і d₂ — довжини діагоналей чотирикутника; α — кут між ними.

Площа паралелограма

де γ — кут між суміжними сторонами а і b.

Площа трапеції

де а і b — основи трапеції; h — її висота.