Основні поняття планіметрії. Трикутники та їхні властивості (част.1)

Планіметрія — розділ геометрії, в якому вивчаються властивості ліній і фігур на площині.

Початкові поняття геометрії, такі як «площина», «пряма», «точка», «лінія», «фігура», належать до неозначуваних.

Твердження в геометрії мають форму означень, аксіом і теорем. Означення розкривають зміст геометричних понять, аксіоми являють собою твердження, прийняті без доведення, а теореми — твердження, які доводять за допомогою логічних міркувань.

Рухом називається перетворення площини, що зберігає відстань між будь-якими двома точками.

Фігури на площині називаються рівними, якщо існує рух, який переводить одну фігуру в іншу.

Сформулюємо деякі основні означення планіметрії, пов’язані з трикутником.

Трикутником, називається фігура, яка складається з трьох відрізків, що попарно сполучають три точки, що не лежать на одній прямій.

Периметром Р трикутника називається сума довжин сторін цього трикутника.

Медіаною трикутника називається відрізок, що сполучає вершину трикутника із серединою протилежної сторони.

Висотою трикутника називається відрізок перпендикуляра, опущеного з вершини трикутника на протилежну сторону чи на її продовження.

Бісектрисою кута називається пряма, що поділяє кут на два рівних кути. 

Бісектрисою трикутника називається відрізок бісектриси кута трикутника, розміщений усередині трикутника.

Прямокутним називається трикутник, дві сторони якого взаємно перпендикулярні (утворюють кут 90°). Дві взаємно перпендикулярні сторони прямокутного трикутника називаються катетами, а третя сторона — гіпотенузою.

Основні ознаки рівності довільних трикутників

Перша ознака. Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то ці трикутники рівні.

Друга ознака. Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам іншого трикутника, то ці трикутники рівні.

Третя ознака. Якщо три сторони одного трикутника дорівнюють трьом сторонам іншого, то ці трикутники рівні.

Теорема 1 (нерівність трикутника). Сума довжин будь-яких двох сторін трикутника більша за довжину третьої сторони.

Зауваження. У деяких курсах планіметрії нерівність трикутника розглядається як аксіома.

Співвідношення між сторонами і кутами в довільному трикутнику визначаються теоремами 2 і 3.

Теорема 2. У трикутнику проти більшої сторони лежить більший кут.

Теорема 3. У трикутнику проти більшого кута лежить більша сторона.

Рівнобедреним називається трикутник, дві сторони якого рівні. Третя сторона рівнобедреного трикутника називається його основою.

Теорема 4. Кути при основі рівнобедреного трикутника рівні.

Обернена теорема: якщо кути при основі трикутника рівні, то трикутник рівнобедрений.

Рівностороннім називається трикутник, усі сторони якого рівні. Усі кути рівностороннього трикутника рівні 60°.

Паралельність

Паралельними називаються дві прямі, що належать одній площині і не мають спільних точок.

Аксіома паралельності (постулат Евкліда). Через точку, що не лежить на даній прямій, можна провести єдину пряму, паралельну даній.

При перетині двох прямих а і b січною утворюється вісім кутів (рис. 1), що мають спеціальні назви:

1) внутрішні односторонні кути 3 і5,4 і6; 2)внутрішні різносторонні кути 4 і5,3 і6; 3) зовнішні односторонні кути1 і8;2 і7; 4) зовнішні різносторонні кути1 і7;2 і 8; 5)відповідні кути 2 і6;4 і7.

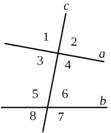
Рис. 1

Ознаки паралельності

1. Якщо при перетині двох прямих третьою внутрішні (зовнішні) різносторонні кути рівні, то прямі паралельні.

2. Якщо при перетині двох прямих третьою відповідні кути рівні, то прямі паралельні.

3. Якщо при перетині двох прямих третьою сума внутрішніх (зовнішніх) односторонніх кутів дорівнює 180°, то прямі паралельні.

Властивості паралельних прямих формулюються як твердження, обернені до ознак. Наприклад: Якщо дві паралельні прямі перетинаються третьою, то внутрішні (зовнішні) різносторонні кути рівні.

Наведемо теореми і означення, пов’язані з паралельністю прямих.

Теорема 1. Сума внутрішніх кутів трикутника дорівнює 180°.